Mathematical modeling and thermodynamic properties for drying soybean grains

Jaqueline Ferreira Vieira Bessa
IF Goiano, Rodovia Sul Goiana, Km 01. Zona Rural. C. Postal 66, Rio Verde ? GO, Brazil.
Search for this author on:
Google Scholar

Adrieli Nagila Kester

Adrieli Nagila Kester
IF Goiano, Rodovia Sul Goiana, Km 01. Zona Rural. C. Postal 66, Rio Verde ? GO, Brazil.
Search for this author on:
Google Scholar

Thais Adriana Souza Smaniotto

Thais Adriana Souza Smaniotto
IF Goiano, Rodovia Sul Goiana, Km 01. Zona Rural. C. Postal 66, Rio Verde ? GO, Brazil.
Search for this author on:
Google Scholar

Article Number - 24D42F749387
Vol.10(1), pp. 31-38 , January 2015
https://doi.org/10.5897/AJAR2014.8711

Received: 17 March 2014
Accepted: 15 May 2014
Published: 01 January 2015

Copyright © 2025 Author(s) retain the copyright of this article.
This article is published under the terms of the Creative Commons Attribution License 4.0.

ABSTRACT

The aims of this work were to adjust different mathematical models to experimental data describing the drying of the Valiosa cultivar soybean grain, to determine and to evaluate the effective diffusion coefficient and to obtain the activation energy and the thermodynamic properties of the drying process under different air conditions. The Valiosa cultivar soybean grains, with an initial moisture content on a dry basis of 0.56 (d.b., decimal), were dried in an oven with forced air ventilation at five different temperatures (40, 55, 70, 85 and 100°C) until reaching a moisture content of 0.133 ± 0.019 (d.b.). Of the models analyzed, Page’s model was selected to best represent the drying phenomenon. The effective diffusion coefficient of soybeans increased with the air temperature and was described by the Arrhenius equation; an activation energy of 22.77 kJ mol^-1 was reported for liquid diffusion in the drying of the soybeans. The enthalpy and entropy decreased with increasing temperature, while the Gibbs free energy increased with increasing drying temperature.

Key words: Glycine max, liquid diffusivity, enthalpy, entropy, Gibbs free energy.

INTRODUCTION

The soybean (Glycine max) is the most commonly grown oilseed in the world because of its high protein content, which is important for the diets of humans and animals raised for human consumption (Carvalho, 2012). The soybean culture is one of the most important cultures in Brazil, as it corresponds to 40% of the total grain produced in the country and 27% of the grain produced worldwide. Brazil is the second largest producer and the largest exporter of soybeans, and this culture account for 20% of exports in Brazilian agribusiness (Vernetti and Vernetti Junior, 2009).

The purpose of drying agricultural products is to ensure their quality, as the reduction in the moisture content reduces the biological activity, chemical and physical changes that occur The study of drying provides information on the heat and mass transfer that occur between the biological material and the drying element (usually heated or non-heated atmospheric air), which is crucial for the design, operation and simulation of drying systems and dryers (Corrêa et al., 2003). The use of mathematical models to simulate the drying process in dryers that operate at high during storage. The study of drying provides information on the heat and mass transfer that occur between the biological material and the drying element (usually heated or non-heated atmospheric air), which is crucial for the design, operation and simulation of drying systems and dryers (Corrêa et al., 2003). The use of mathematical models to simulate the drying process in dryers that operate at high temperatures is an important tool for engineers who work in the field of drying and storage of grains.

The liquid diffusion theory has been widely used to study the drying of vegetable products. According to Corrêa et al. (2006), the liquid diffusion mechanism is complex because of the diversity in chemical compositions and physical structures of the product. Water diffusion in agricultural products involves different mechanisms, including molecular diffusion, capillary diffusion, surface diffusion, hydrodynamic flow, vapor diffusion and thermal diffusion (Goneli et al., 2009).

Knowledge of the thermodynamic properties involved in the drying of agricultural products allows engineers to design better drying equipment, to calculate energy requirements necessary for the process, to study the properties of adsorbed water, to evaluate the microstructure of food and to study the physical phenomena that occur at the material surface (Corrêa et al., 2010). The aims of this study was to obtain, model the drying curves, evaluate the liquid diffusion and the thermodynamic properties of Valiosa cultivar soybean grains dried under different air-drying conditions.

MATERIALS AND METHODS

The experiments were conducted in the Laboratory for the Postharvest of Vegetables Products (Laboratório de Pós-colheita de Produtos Vegetais) at the Federal Institute of Education, Science and Technology of Goiás (Instituto Federal de Educação, Ciência e Tecnologia Goiano – Câmpus Rio Verde) with Valiosa cultivar soybean grains from the municipality of Santa Helena de Goiás (GO). The initial moisture content of the grains was 0.56 (d.b., decimal); these grains were dried in an oven with forced air ventilation at five different temperatures (40, 55, 70, 85 and 100°C), leading to relative humidities of 25.3, 12.5, 5.7, 3.5 and 2.2%, respectively. The drying continued until the grain moisture content reached 0.133 ± 0.019 (d.b.), determined at 105 ± 1°C for 24 h in three replicates (Brasil, 2009). The reduction in the moisture content during drying was monitored with the gravimetric method (mass loss) using an analytical balance with a resolution of 0.01 g installed on the outside of the oven; knowing the initial moisture content of the product, the drying continued until the desired moisture content was achieved.

The temperature and relative humidity of the external ambientenvironment of the drying chamber were monitored with a psychrometer, using a thermometer with dry bulb and another with wet bulb, and the internal temperature was monitored with a thermometer installed inside the oven. The relative humidity of the drying air was obtained by means of the basic principles of psychrometry, using the free software GRAPSI.

The moisture content ratios of the soybeans during drying were determined with the following expression:

where, RX: ratio of the moisture content of the product, dimensionless; X: moisture content of the product (d.b., decimal); X_i: initial moisture content of the (d.b., decimal); and X_e: equilibrium moisture content of the product (d.b., decimal).

The equilibrium moisture content of the soybeans at each temperature was obtained with the modified version of Henderson's equation, as reported by ASAE (1988). The experimental data describing the drying process of the soybeans were adjusted with mathematical models commonly used to represent the drying of agricultural products; these models are presented in Table 1.

The mathematical models were fitted using nonlinear regression with the Gauss-Newton method using software Statistica 7.0. The models were selected according to the determination coefficient (R² in %) and the relative average error (P in %). A relative average error of less than 10% was considered a criterion for model selection, as recommended by Mohapatra and Rao (2005).

where, D_o: pre-exponential factor; E_a: activation energy, kJ mol^-1; R: universal gas constant, 8.134 kJ kmol^-1K^-1; and T_ab:

absolute temperature, K.

The thermodynamic properties of the drying of soybean grains were obtained with the method reported by Jideani and Mpotokwana (2009):

where, ?H = enthalpy, J mol^-1; ?S = entropy, J mol^-1; ?G = Gibbs free energy, J mol^-1; k_B = Boltzmann constant, 1.38 x 10^-23 J K^-1; and h_p = Planck constant, 6.626 x 10^-34 J s^-1.

RESULTS AND DISCUSSION

The average values of the moisture content ratio of the soybean grains dried under different air conditions are shown in Table 2. The times required for the grains to reach the moisture content of 0.133±0.019 (d.b.) were 18.6, 11.6, 7.7, 5.9 and 4.7 h for the drying temperatures 40, 55, 70, 85 and 100°C, respectively.

The increase in air temperature was found to cause a reduction in the grain drying time. The reduction in drying time is related to the greater difference between the partial pressure of water vapor in the drying air and in the product caused by the increase in temperature. This greater difference promotes an easier and more rapid water removal; similar observations were made by other authors for numerous products (Resende et al., 2008; Almeida et al., 2009; Sousa et al., 2011; Costa et al., 2011; Oliveira et al., 2012).

The values ??of the determination coefficient (R²) and the relative average error (P) of the eleven models adjusted during the drying of the soybeans at different temperatures are shown in Table 3. The determination coefficient (R²) was ??above 99% for all models and all drying temperatures, indicating, according to Madamba et al. (1996), a satisfactory representation of the phenomenon under study.

The models presented relative average error values ??(P) less than 10% for the five conditions analyzed, indicating, according to Mohapatra and Rao (2005), that they provide suitable representations of the drying phenomenon. However, the Wang and Sing (2), Newton (4), Exponential of Two Terms (8) and Thompson (12) models had the highest values ??of P. The analyzed models satisfactorily represented the process of soybean grain drying; however, the Page (3), Logarithmic (5) and Midilli (7) models had the best overall fits. Thus, due to its simplicity, the Page model was selected to represent the phenomenon of soybean grain drying.

Figure 1 shows the drying curves for soybean at the different studied temperatures generated from the experimental data ??and the values estimated by the Page model. A satisfactory adjustment of the model to the experimental values obtained over the drying of soybeans.??

The drying time of the product was inversely proportional to the temperature; in other words, the higher the temperature, the shorter the drying time. The drying times for 40 and 100°C were 18.6 and 4.7 h, respectively. Corrêa et al. (2010) reported that the reduction in the moisture content of agricultural products, especially of grains and seeds, occurs with decreasing order with increasing temperature due to the difference in the surface moisture and the size of the whole grain. Sousa et al. (2011) and Oliveira et al. (2012) reported similar results for the drying of forage turnip seeds and corn, respectively.

Table 4 shows the values ??of the coefficients “k” and “n” of the Page model fitted to experimental data describing the kinetics of soybean grain drying at different temperatures.

The magnitude of the drying constant k for the Page model represents the phenomenon whereby temperature increases in the drying air result in increasingly favorable external drying conditions. However, the coefficient n of the Page model was not affected by drying temperature.

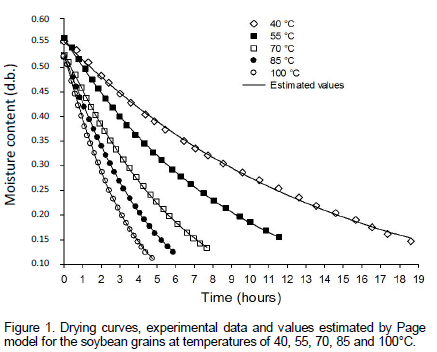
Thus, for the range of temperatures studied, the drying of soybean grains can be estimated using the following expression:

where: T: drying temperature (°C); t: drying time (h).

Figure 2 shows the experimental and the estimated data for the moisture content ratio (RX) obtained using the Page model, the values ??obtained using Equation 9 and the values ??presented in Table 2. This model provided a good adjustment to the data while adequately describing the process of soybean grain drying. The reduction in the moisture content ratio leads to a greater discrepancy between the estimated and experimental values.

The values ??of the effective diffusion coefficient of soybeans as a function of the conditions of the drying air are shown in Figure 3. The effective diffusion coefficient increased linearly with increasing temperature of the drying air, with values ??of 0.847 × 10^-11 to 3.46 × 10^-11m²s^-1 for temperatures ranging from 40 to 100°C, indicating a greater intensity of water transport from the inside to the periphery of the grain and corroborating results obtained by Mohapatra and Rao (2005), Resende et al. (2008), Almeida et al. (2009), Costa et al. (2011), Corrêa et al. (2011) and Siqueira et al. (2012). Madamba et al. (1996) reported that the effective diffusion coefficients were on the order of 10^-11 to 10^-9 m² s^-1.

Sousa et al. (2011) studied the drying of fodder radish seeds and obtained values ??similar to those found in the present work on the order of 3.23 × 10^-11 to 10.42 × 10^-11 m².s^-1at temperatures of 30 and 70°C, respectively. Gely and Santalla (2007) and Oliveira et al. (2012) encountered values on the order of 1.18 × 10^-12 to 6.76 × 10^-12 m².s^-1 and 1.54 × 10^-13 to 4.85 × 10^-13m².s^-1 m².s^-1 for the diffusion coefficients of quinoa seeds and corn grains, respectively. Thus, water is removed more rapidly from soybeans than from quinoa seeds and corn grains.

The dependence of the effective diffusion coefficient of the soybean grains on the drying air temperature was represented by the Arrhenius expression as illustrated in Figure 4. The activation energy is defined as the ease with which water molecules overcome the energy barrier for migration from the interior of the product to its exterior (Resende et al., 2005). In the present work, the activation energy for the liquid diffusion of soybeans was 22.77 kJ.mol^-1 in the studied temperature range. According to Zogzas et al. (1996), the activation energy for agricultural products ranges from 12.7 to 110 kJ.mol^-1; thus, the value obtained in the present study is within this range.

Kitic and Viollaz (1984) obtained a value close to that found in the present work. These authors reported an activation energy for the soybean of 28.80 kJ.mol^-1. Gely and Santalla (2007) and Costa et al. (2011) evaluated the drying of quinoa and crambe and reported activation energies of 37.97 and 37.07 kJ.mol^-1, respectively. The activation energy of soybean encountered in the present study was lower than that found in other studies; this may be due to the more unstable bond between water and the product evaluated, as reported by Siqueira et al. (2012).

Table 5 shows the values ??of enthalpy, entropy and Gibbs free energy for the different drying conditions. The enthalpy and entropy decreased while the Gibbs free energy increased linearly with increasing drying temperature.

The enthalpy is related to the energy required to remove water from the product during the drying process; thus, the enthalpy decreases with increasing drying temperature (Oliveira et al., 2010). This behavior was observed for soybean grains during the reduction of the moisture content, indicating that lower temperatures require more energy.

According to Goneli et al. (2010), the entropy is a thermodynamic property that can be related to the degree of disorder between the water and the product. The entropy decreases with increasing drying air temperature. Corrêa et al. (2010) reported that this behavior is expected because the decrease in drying temperature decreases the excitation of water molecules of the products and increases the order of the water-product system.

The Gibbs free energy is related to the work required to produce available sorption sites (Nkolo Meze’e et al., 2008). The Gibbs free energy can be positive for endogenous reactions where it is necessary to add energy from the environment. The Gibbs free energy can be negative when the phenomenon occurs spontaneously without the addition of energy. The Gibbs free energy of soybean grains was found to be positive and increased with increasing drying temperature. This behavior was also observed by Corrêa et al. (2011) when studying the thermodynamic properties of corn cobs drying at temperatures of 45, 55 and 65°C.

Equations used to determine the enthalpy, the entropy and the Gibbs free energy for the temperature range studied can be found in Table 5. These thermodynamic properties behaved in a linear manner and were characterized by high coefficients of determination.

CONCLUSION

All of the analyzed models satisfactorily represented the drying of grains; however, the Page model, due to its simplicity, was chosen to best represent the phenomenon. The effective diffusion coefficient of soybeans increased with increasing drying air temperature; this phenomenon was described by the Arrhenius equation and characterized by an activation energy of 22.77 kJ.mol^-1.

The enthalpy and entropy decreased with increasing drying temperature and the entropy was negative at all temperatures studied. The Gibbs free energy was positive for the analyzed conditions and increased with increasing drying temperature.

CONFLICT OF INTEREST

The authors have not declared any conflict of interest.

ACKNOWLEDGEMENTS

The authors extend thanks to IF Goiano, FINEP, CAPES and CNPq for their financial support, which was indispensable to the execution of this study.

REFERENCES

Almeida DP, Resende O, Costa LM, Mendes UC, Sales JF (2009). Cinética de secagem do feijão adzuki (Vigna angularis) [Drying kinetics of adzuki beans (Vigna angularis)]. Global Sci. Technol. 2:72-83.

American Society of Agricutural Engineers (ASAE) (1988). Agricultural Engineers Handbook. ASAE, (35th), St. Joseph. Brasil, Ministério da Agricultura e Reforma Agrária. Secretaria Nacional de defesa Agropecuária (2009). Regras para Análise de Sementes [Regulations for Testing Seeds]. (1th ed.). Brasília.

Brooker DB, Bakker-Arkema FW, Hall CW (1992). Drying and storage of grains and oilseeds. Westport: The AVI Publishing Company. P. 450.

Carvalho PT (2012). Balanço de emissões de gases de efeito estufa de biodiesel produzido a partir de soja e dendê no Brasil [Balance of emissions of greenhouse gases from biodiesel produced from soybean oil and palm oil in Brazil]. Thesis (Master) presented to the the Graduate Program in Energy Planning, COPPE, Federal University of Rio de Janeiro.

Corrêa PC, Araújo EF, Afonso Júnior PC (2003). Determinação dos parâmetros de secagem em camada delgada de sementes de milho doce (Zea mays L.) [Determination of the parameters related to thin-layer drying of sweet corn seeds (Zea mays L.)]. Rev. Bras. Milho Sorgo 2:110-119.

Corrêa PC, Resende O, Goneli ALD, Botelho FM, Nogueira BL (2006). Determinação do coeficiente de difusão liquida dos grãos de feijão [Determination of the liquid diffusion coefficient of bean grains]. Rev. Bras. Produtos Agroindust. 8:117-126.

Corrêa PC, Oliveira GHH, Botelho FM, Goneli ALD, Carvalho FM (2010). Modelagem matemática e determinação das propriedades termodinâmicas do café (Coffea arábica L.) durante o processo de secagem [Mathematical modeling and determination of the thermodynamic properties of coffee (Coffea arabica L.) during the drying process]. Rev. Ceres 57:595-601. CrossRef

Corrêa PC, Botelho FM, Oliveira GHH, Goneli ALD, Resende O, Campos SC (2011). Mathematical modeling of the drying process of corn ears. Acta Scientiarum-Agronomy 33:575-581. CrossRef

Costa LM, Resende O, Sousa KA, Gonçalves DN (2011). Coeficiente de difusão efetivo e modelagem matemática da secagem de sementes de crambe [Effective diffusion coefficient and mathematical modeling of the drying of crambe seeds]. Rev. Bras. Engenharia Agríc. Ambiental 15:1089-1096. CrossRef

Gely MC, Santalla EM (2007). Moisture diffusivity in quinoa (Chenopodium quinoa Willd.) seeds: Effect of air temperature and initial moisture content of seeds. J. Food Eng. 78:1029-1033. CrossRef

Goneli ALD, Corrêa PC, Afonso Júnior PC, Oliveira GHH (2009). Cinética de secagem dos grãos de café descascados em camada delgada [Kinetics of thin-layer drying of peeled coffee beans]. Revista Brasileira de Armazenamento special Coffe pp. 64-73.

Goneli ALD, Corrêa PC, Oliveira GHH, Botelho FM (2010). Water desorption and thermodynamic properties of okra seeds. Transactions of the ASAE 53:191-197. CrossRef

Henderson SM (1974). Progress in developing the thin layer drying equation. Transactions of the ASAE 17:1167-1168. CrossRef

Henderson SM, Pabis S (1961). Grain drying theory: temperature effect on drying coefficient. J. Agric. Eng. Res. 6:169-174.

Jideani VA, Mpotokwana SM (2009). Modeling of water absorption of botswana bambara varieties using Peleg's equation. J. Food Eng. 92:182–188. CrossRef

Kassem AS (1998). Comparative studies on thin layer drying models for wheat. In: International Congress on Agricultural Engineering, 13th., Morocco. [Holdings]. Morocco: [s. n.]. P. 06.

Kitic D, Viollaz PE (1984). Comparison of drying kinetic of soybean in thin layer and fluidized beds. J. Food Technol. 19:399-408. CrossRef

Lewis WK (1921). The drying of solid materials. J. Ind. Eng. Chem. 13:427-433. CrossRef

Madamba PS, Driscoll RH, Buckle KA (1996). Thin-layer drying characteristics of garlic slices. J. Food Eng. 29:75-97. CrossRef

Midilli A, Kucuk H, Yapar Z (2002). A New model for single layer drying. Drying Technol. 20:1503-1513. CrossRef

Mohapatra D, RAO PS (2005). A thin layer drying model of parboiled wheat. J. Food Eng. 66:513-518. CrossRef

Mohsenin NN (1986). Physical properties of plant and animal materials. (1th ed.) New York: Gordon and Breach Publishers.

Nkolo Meze'e YN, Noah Ngamveng J, Bardet S (2008). Effect of enthalpy–entropy compensation during sorption of water vapour in tropical woods: the case of bubinga (Guibourtia Tessmanii J. L´Eonard; G. Pellegriniana J.L.). Thermochim. Acta 468:1-5. CrossRef

Oliveira DEC, Resende O, Smaniotto TAS, Campos RC, Chaves TH (2012). Cinética dos grãos de milho [Kinetics of corn grains]. Rev. Bras. Milho Sorgo 11:189-201.

Oliveira GHH, Corrêa PC, Araújo EF, Valente DSM, Botelho FM (2010). Desorption isotherms and thermodynamic properties of sweet corn cultivars (Zea mays L.). Int. J. Food Sci. Technol. 45:546-554. CrossRef

Page GE (1949). Factors influencing the maximum rates of air drying shelled corn in thin layers. West Lafayette: Purdue University.

Resende O, Corrêa PC, Goneli ALD, Botelho FM, Rodrigues S (2008). Modelagem matemática do processo de secagem de duas variedades de feijão (Phaseolus vulgaris L.) [Mathematical modeling of the drying process of two varieties of common bean (Phaseolus vulgaris L.)]. Rev. Bras. Prod. Agroind. 10:17-26.

Resende O, Corrêa PC, Goneli ALD, Martinazzo AP, Ribeiro RM (2005). Contração volumétrica na difusão líquida durante o processo de secagem do arroz em casca [Volumetric contraction in liquid diffusion during the drying of paddy rice]. Rev. Bras. Armazenamento 30:163-171.

Sharaf-Eldeen YI, Blaisdell JL, Hamdy MY (1980). A model for ear corn drying. Transactions of the ASAE 23:1261-1265. CrossRef

Siqueira VC, Resende O, Chaves TH (2012). Difusividade efetiva de grãos e frutos de pinhão-manso [Effective diffusivity of grains and fruits of Jatropha curcas]. Semina: Ciênc. Agrárias 33:2919-2930. CrossRef

Sousa KA, Resende O, Chaves TH, Moreira LC (2011). Cinética de secagem do nabo forrageiro (Raphanus sativus L.) [Drying kinetics of forage turnips (Raphanus sativus L.)]. Rev. Ciênc. Agron. 42:883-892. CrossRef

Thompson TL, Peart RM, Foster GH (1968). Mathematical simulation of corn drying: a new model. Transactions of ASAE 11:582-586. CrossRef

Verma LR, Bucklin RA, Endan JB, Wratten FT (1985). Effects of drying air parameters on rice drying models. Transactions of the ASAE 28:296-301. CrossRef

Vernetti F de J, Vernetti Junior F de J (2009). Genética da Soja: Caracteres Qualitativos e Diversidade Genética [Soybean Genetics: Genetic Diversity and Qualitative Characteristics]. Embrapa Inform. Tecnológica, Brasília: DF.

Zogzas NP, Maroulis ZB, Marinos-Kouris D (1996). Moisture diffusivity data compilation in foodstuffs. Dry. Technol. 14:2225-2253. CrossRef

Yagcioglu A, Degirmencioglu A, Cagatay F (1999). Drying characteristics of laurel leaves under different conditions. In: International Congress on Agricultural Mechanization and Energy, 7th., Adana. Proceedings. Adana: Cukurova University, pp. 565-569.

Wang CY, Singh RP (1978). Use of variable equilibrium moisture content in modeli

This article is published under the terms of the Creative Commons Attribution License 4.0

Back to Vol. 10 No. 1

Back to articles

Views: 0
Downloads: 0

Related Articles:
On Google
On Google Scholar

African Journal of Agricultural Research